Pada materi ini saya akan menjelaskan cara perhitungan metode weighted product dimana proses dalam perhitungan tersebut dengan menghitung pembobotan pada setiap kriteria yang telah di tentukan, contoh kali ini untuk menghitung penentuan beasiswa untuk sekolah. Berikut adalah contoh perhitungan yang telah saya ringkas.
Kriteria yang digunakan sebagai acuan dalam pemlihan beasiswa yang berhak mendapatkan beasiswa ada 4 yaitu :
Kode
|
Kriteria
|
C1
|
Jumlah anak dalam keluarga
|
C2
|
Nilai Rata – Rata Rapot
|
C3
|
Penghasilan Orang Tua
|
C4
|
Rata – Rata Biaya Listrik Perbulan
|
Pada kriteria diatas ditentukan pengambil keputusan sebagai bobot untuk setiap kriteria, penentuan bobot ini bisa anda tentukan sendiri atau ditentukan oleh objek penelitan anda :
Kriteria
|
Variabel
|
Kriteria Bobot
|
Bobot
|
Nilai Minimal Bobot
|
C1
|
Jumlah anak dalam keluarga
|
< 2
|
3
|
3
|
= 2
|
4
| |||
>2
|
5
| |||
C2
|
Nilai Rata – Rata Rapot
|
<=5.00
|
1
|
4
|
5.10 – 6.00
|
2
| |||
6.10 – 7.00
|
3
| |||
7.10 – 8.00
|
4
| |||
>=8.10
|
5
| |||
C3
|
Penghasilan Orang Tua
|
<= 1 juta
|
5
|
5
|
1.1 – 1.5 juta
|
4
| |||
1.6 – 2 juta
|
3
| |||
2.1 – 2.5 juta
|
2
| |||
2.6 – 3 juta
|
1
| |||
C4
|
Rata – Rata Biaya Listrik Perbulan
|
>75000
|
2
|
3
|
=75000
|
3
| |||
<75000
|
5
|
Yang perlu anda perhatikan adalah pada proses penentuan nilai bats minimal bobot, pada kasus diatas saya penentukan batas bobot untuk setiap kriteria C1= 3, C2= 4, C3=5, C6=3.
Kemudian misal ada 30 siswa yang telah terinput datanya digambarkan pada tabel berikut ini :
ALTERNATIF
|
KRITERIA
| |||
C1
|
C2
|
C3
|
C4
| |
A1
|
3
|
1
|
4
|
2
|
A2
|
3
|
1
|
4
|
2
|
A3
|
5
|
5
|
4
|
5
|
A4
|
5
|
4
|
3
|
5
|
A5
|
5
|
4
|
5
|
5
|
Langkah pertama yang harus dilakukan yaitu dengan menghitung perbaikan bobot batas nilai, batas nilai yang telah kita tentukan sebelumnya yaitu : 3, 4, 5, 3
Dengan rumus :
Keterangan :
Setiap bobot dilakukan perhitungan perbaikan bobot terlebih dahulu
Dari hasil diatas didapatkan nilai W1 - W4 dimana hasil tersebut adalah perwakilan dari setiap kriteria, dan kriteria telah ditentukan ada 4 kriteria. Kemudian dari hasil W tersebut akan dijadikan nilai pangkat pada setiap data 30 siswa yang telah kita tentukan sebelumnya dengan menentukan nilai vektor S.
Rumus menghitung nilai vektor S :
Dari rumus diatas maka di dapatkan hasil perhitungan pembobotan dari 30 data sebagai berikut :
S1=(3^0.2 )*(1^0.26 )*(4^0.33 )*(2^0.2 )= 2.62
S2=(3^0.2 )*(1^0.26 )*(4^0.33 )*(2^0.2 )= 2.62
S3=(5^0.2 )*(5^0.26 )*(4^0.33 )*(5^0.2 )= 4.72
S4=(5^0.2 )*(4^0.26 )*(3^0.33 )*(5^0.2 )= 4.28
S5=(5^0.2 )*(4^0.26 )*(5^0.33 )*(5^0.2 )= 4.72
S6 ( batas nilai ) = (3^0.2 )*(4^0.26 )*(5^0.33 )*(3^0.2 )= 3.87
ket :
^ = pangkat
Jumlah yang di hitung 30 data + batas nilai. Yang saya maksud disini adalah batas nilai juga ikut di hitung, untuk menentukan hasil nilai dari batas nilai tersebut. Setiap jumlah data jangan lupa di ikuti dengan menghitung batas nilai yang telah di tentukan.
Langkah selanjutnya yaitu menghitung nilai vektor, untuk proses perangkingan data. Brikut adalah rumus untuk menentukan nilai vektor
Rumus sederhananya sebagai berikut :
Dan berikut ini adalah hasil perhitungan dari 5 data dari rumus nilai vektor tersebut :
Dari hasil diatas penentuan nilai yang lolos yaitu dimana nilai yang => V6 (batas nilai ) atau nilai yang => 0.169513798 di nyatakan lolos, di nilai dibawah itu dinyatan tidak lolos.
Contoh di atas adalah cara perhitungan metode weighted product, cukup mudah dan simple. Kuncinya setiap jumlah data yang di hitung atau setiap penambahan data maka hasil perhitungan metode weighted product akan selalu berubah, karena jumlah pembagi juga akan betambah. Dan jangan lupa setiap melakukan perhitungan batas nilai harus selalu di ikut sertakan untuk menjadi acuan nilai standart minimal / nilai kelolosan.
Jika ada pertanyaan atau koreksi perhitungan silahkan sampaikan melalui kolom komentar.






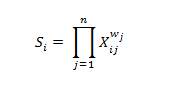







Post a Comment
Post a Comment